「雅礼集训 2018-04-02」Problem B

发表于

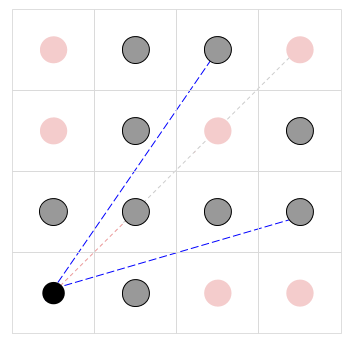
有一个长宽均为 NN 的网格，每个格子的长宽均为 11。除了最左下角的网格外，其他格子中均有一个半径为 RR 的圆，圆心在格子的正中心。现在你站在最左下角的格子的正中心，求你能够看到多少个圆，视线不能够穿过圆。

输入一行包含两个整数 NN ，R0R_0 ，题目中的 RR 为R0106\frac{R_0}{10^6} 。

avatar

Constraints

$ n \leq 10^9$ ， R0≤106R_0 \leq 10^6

Solution

首先可以确定一个结论：只有能够看到圆心才能够看到这个圆。

枚举圆 (x,y)(x,y) 和圆 (a,b)(a,b) ，根据点到直线的距离公式 ∣Ax0+By0+CA2+B2∣\begin{vmatrix} \frac{Ax_{0}+By_{0}+C}{\sqrt{A^{2}+B^{2}}} \end{vmatrix} ，可得若 (a,b)(a,b) 挡住了 (x,y)(x,y) ，则 (ay−bx)2x2+y2≤R2\frac{(ay-bx)^{2}}{x^{2}+y^{2}}\leq R^{2} 。

只考虑 x,yx,y 互质的情况，那么一定存在 a<xa<x ， b<yb<y ， ∣ay−bx∣=1|ay-bx|=1 ，这时候只要满足 x2+y2<1R2x^{2}+y^{2}< \frac{1}{R^{2}} 就不会被挡住。

所以令 r=1Rr=\frac{1}{R} ，枚举约数 dd ，得出：

∑d=1min(n,r)μ(d)∑x=1⌊rd⌋∑y=1⌊rd⌋[x2+y2<r2d2]\sum _{d=1}^{min(n,r)}\mu(d)\sum _{x=1}^{\lfloor \frac{r}{d} \rfloor}\sum _{y=1}^{\lfloor \frac{r}{d} \rfloor}[x^{2}+y^{2}<\frac{r^{2}}{d^{2}}]

具体计算方式见代码。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
using namespace std;
const int N=1e6+5;
int n,r,tot,pri[N],miu[N];
LL ans;
bool np[N];
LL calc(LL lim,LL n)
{
    LL y=sqrt(lim)+1,sum=0;
    y=min(y,n);
    for(LL x=1;x*x<lim&&x<=n;x++)
    {
        while(y&&x*x+y*y>lim)y--;
        sum+=y;
    }
    return sum;
}
int main()
{
    miu[1]=1;
    for(int i=2;i<=1e6;i++)
    {
        if(!np[i]){miu[i]=-1;pri[++tot]=i;}
        for(int j=1;i*pri[j]<=1e6;j++)
        {
            int now=i*pri[j];
            np[now]=true;
            if(i%pri[j]==0){miu[now]=0;break;}
            miu[now]=-miu[i];
        }
    }
    scanf("%d%d",&n,&r);
    LL lim=1ll*999999999999/r/r;
    for(LL g=1;g*g<=lim;g++)
        ans+=miu[g]*calc(lim/g/g,(n-1)/g);
    printf("%lld",ans+2);
    return 0;
}