「LOJ 2083」「NOI2016」优秀的拆分

发表于

如果一个字符串可以被拆分为 AABB\text{AABB} 的形式，其中 A\text{A} 和 B\text{B} 是任意非空字符串，则我们称该字符串的这种拆分是优秀的。

一个字符串可能没有优秀的拆分，也可能存在不止一种优秀的拆分。

现在给出一个长度为 nn 的字符串 SS，我们需要求出，在它所有子串的所有拆分方式中，优秀拆分的总个数。这里的子串是指字符串中连续的一段。

以下事项需要注意：

  • 出现在不同位置的相同子串，我们认为是不同的子串，它们的优秀拆分均会被记入答案。
  • 在一个拆分中，允许出现 A=B\text{A}=\text{B} 。
  • 字符串本身也是它的一个子串。

Constraints

$ 1 \leq T \leq 10$ ， 1≤n≤300001 \leq n \leq 30000

Solution

我们以 ABAB 为分界线，只需求出分界线左右的 AAAA 串然后组合即可。

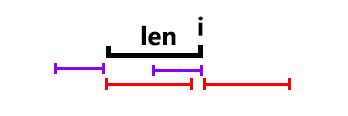
考虑枚举长度 lenlen ，对于两个位置 ii 与 i−leni-len ，求出向前的最长公共后缀和向后的最长公共前缀（二分 + 哈希），组合可以得到一个长度为 2⋅len2\cdot len 的 AAAA 串。具体的结尾有效区间为 [i−lsp+len,i+lcp−1][i-lsp+len,i+lcp-1] ，需要注意边界。

avatar

时间复杂度 O(nlog2n)O(nlog^2n) 。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
using namespace std;
const int N=3e4+5;
const int mod=998244353;
int T,n,l,r,mid,last,cur,head,tail;
LL ans,bit[N],h[N],st[N],ed[N];
char s[N];
LL gethash(int L,int R){return (h[R]-h[L-1]*bit[R-L+1]%mod+mod)%mod;}
int main()
{
	scanf("%d",&T);bit[0]=1;
	for(int i=1;i<=30000;i++)
		bit[i]=bit[i-1]*29%mod;
	while(T--)
	{
		scanf("%s",s+1);n=strlen(s+1);
		for(int i=1;i<=n;i++)h[i]=(h[i-1]*29+s[i]-'a')%mod;
		memset(st,0,sizeof(st));
		memset(ed,0,sizeof(ed));
		for(int len=1;len*2<=n;len++)
			for(int i=len*2;i<=n;i+=len)
			{
				if(s[i]!=s[i-len])continue;
				last=i-len;cur=0;l=1;r=i-len;
				while(l<=r)
				{
					mid=(l+r)>>1;
					if(gethash(last-mid+1,last)==gethash(i-mid+1,i))cur=mid,l=mid+1;
					else r=mid-1;
				}
				head=max(i-cur+len,i);
				l=1;r=n-i+1;cur=0;
				while(l<=r)
				{
					mid=(l+r)>>1;
					if(gethash(last,last+mid-1)==gethash(i,i+mid-1))cur=mid,l=mid+1;
					else r=mid-1;
				}
				tail=min(i+cur-1,i+len-1);
				if(head<=tail)
				{
					st[head-len*2+1]++;st[tail-len*2+2]--;
					ed[head]++;ed[tail+1]--;
				}
			}
		ans=0;
		for(int i=1;i<=n;i++)st[i]+=st[i-1],ed[i]+=ed[i-1];
		for(int i=1;i<n;i++)ans+=ed[i]*st[i+1];
		printf("%lld\n",ans);
	}
	return 0;
}