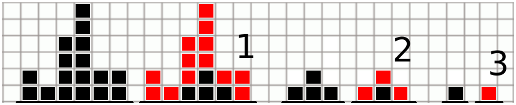
有 堆方块,第 堆方块由 个方块堆积而成。
接下来拆方块。一个方块称为内部方块当且仅当他的上下左右都是方块或者是地面。否则方块就是边界方块。每一次操作都要把边界方块拿掉。
问多少次操作之后所有方块会消失。
Constraints
Solution
观察可得,每一轮进行的操作为 。当一列方块被拆掉时,下一轮他的相邻两列中未被拆掉的列也会被拆掉。
从左往右和从右往左分别扫一遍,取 min 即是当前列被拆掉的操作次序。时间复杂度 。
Code
1 |
|
Living is do or die.
有 n 堆方块,第 i 堆方块由 hi 个方块堆积而成。
接下来拆方块。一个方块称为内部方块当且仅当他的上下左右都是方块或者是地面。否则方块就是边界方块。每一次操作都要把边界方块拿掉。
问多少次操作之后所有方块会消失。

1≤n≤105
观察可得,每一轮进行的操作为 hi=min(hi−1,hi−1,hi+1) 。当一列方块被拆掉时,下一轮他的相邻两列中未被拆掉的列也会被拆掉。
从左往右和从右往左分别扫一遍,取 min 即是当前列被拆掉的操作次序。时间复杂度 O(n) 。
1 | #include<cstdio> |